| |
4-6 堆疊資料結構
內容:
4-6-1 陣列堆疊結構
堆疊(Stack)在資訊系統裡時常用到,與 Queue 一樣都是屬於排列順序裝置,但他的順序是『先進後出』(First-In-Last-Out, FILO),表示先來的後出去的意思。圖 4-20 是Stack 的儲存結構,他只有一個出入口,資料進出都由這個口,地多利用 Top 變數來指示目前出入口位置。另外利用 push() 方法來操作將資料推入堆疊內(Top = Top + 1),與pop() 方法將資料由堆疊內擠出(Top = Top – 1)。
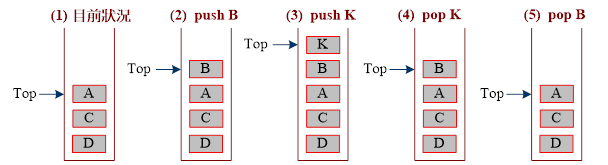
圖 4-20 Stack 的運作程序
4-6-2
範例研討:走迷宮演練
(A) 程式功能:Ex4_7.java
談到堆疊(Stack)大多人都會想到走迷宮的問題,但其實它應用非常廣泛,譬如導航系統一定都會用到。吾人利用堆疊記錄過去走的路徑,當須退回原處時,再依照堆疊內記錄退回原處,就不會迷路了。
圖 4-21 是迷宮地圖,吾人將地圖中每一個節點都用座標表示,橫座標由 A ~ Q,縱座標由 0 ~9,位置由 A0 ~ Q9,並所有路徑(或位置)都可以通過。假設,我們由 D9 開始,經過圖中節點到達 Q0,回程由 Q0 是否可以回到 D9。
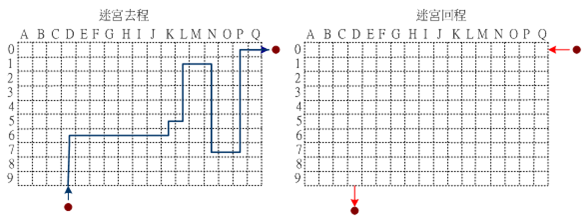
圖 4-21 迷宮走路演練
請編寫一只程式依照圖中路徑行走,完畢後再顯示所經過的節點如何,接著再依照走過的記錄是否可以回到原點,驗證走迷宮的初步構想。期望功能如下:
(1) 期望具有以下 4 種功能,選單如下:
|
D:\Java2_book\chap4>javac Ex4_7.java
D:\Java2_book\chap4>java Ex4_7
== 歡迎光臨 走迷宮演練 ==
(1) 列印以走過的路線
(2) 迷宮去程開始
(3) 迷宮回程開始
(4) 離開系統
請輸入工作選項 => |
(2) 當選擇迷宮去程(選擇 2與 1),則出現走過路線如下:
|
請輸入工作選項 =>2
D0 ==> D9 ==> D8 ==> D7 ==> E7 ==>
F7 ==> G7 ==> H7 ==> I7 ==> J7 ==>
K7 ==> K6 ==> L6 ==> L5 ==> L4 ==>
L3 ==> L2 ==> M2 ==> N2 ==> N3 ==>
N4 ==> N5 ==> N6 ==> N7 ==> N8 ==>
O8 ==> P8 ==> P7 ==> P6 ==> P5 ==>
P4 ==> P3 ==> P2 ==> P1 ==> Q1 ==>
總共走了 35 路徑 |
(3)
選擇查閱過去走的路線(選擇 1),如下:
|
請輸入工作選項 =>1
== 到目前經過 35 個路徑 ==
(1)D0 (2)D9 (3)D8 (4)D7 (5)E7
(6)F7 (7)G7 (8)H7 (9)I7 (10)J7
(11)K7 (12)K6 (13)L6 (14)L5 (15)L4
(16)L3 (17)L2 (18)M2 (19)N2 (20)N3
(21)N4 (22)N5 (23)N6 (24)N7 (25)N8
(26)O8 (27)P8 (28)P7 (29)P6 (30)P5
(31)P4 (32)P3 (33)P2 (34)P1 (35)Q1 |
(4)
當選擇迷宮回程(選擇 3 ),則會依照之前走過路徑回到原地,如下:
|
請輸入工作選項 =>3
Q1 ==> P1 ==> P2 ==> P3 ==> P4 ==>
P5 ==> P6 ==> P7 ==> P8 ==> O8 ==>
N8 ==> N7 ==> N6 ==> N5 ==> N4 ==>
N3 ==> N2 ==> M2 ==> L2 ==> L3 ==>
L4 ==> L5 ==> L6 ==> K6 ==> K7 ==>
J7 ==> I7 ==> H7 ==> G7 ==> F7 ==>
E7 ==> D7 ==> D8 ==> D9 ==> D0 ==>
回程路徑已結束 |
(B) 系統分析
首先我們宣告陣列 path[],並依照圖4-21(a) 路徑位置填入該陣列。前進時,由 path[] 中讀取下一個路徑位置,並將該位置推入(Push)堆疊內,一直到讀取完畢,表示已走完所有路徑,堆疊內也記錄所有走過的節點。回程時,再一個接一個位置由堆疊內擠出(Pop),依照擠出位置行走,就可以回到原點。
(C) 程式範例
圖 4-22 為其程式架構,我們將 Push 與 Pop 製作成獨立的方法,可利用他們對 Stack 做推入與擠出的操作。
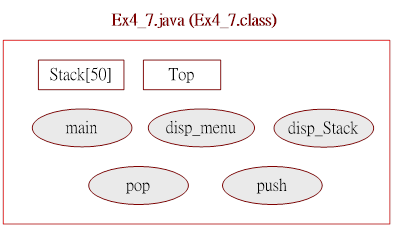
圖 4-22 Ex4_7 程式架構
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95 |
//Ex4_7.java
/*
走迷宮演練(驗證 Stack
功能) */
import java.util.*;
public class Ex4_7{
static String Stack[] = new String[50]; //
宣告佇列空間
static int Top; //
宣告佇列後端
public static void main(String args[]) {
Scanner keyin = new Scanner(System.in);
Top = -1; //
佇列初值,表示佇列空閒
String step;
String path[] = {"D0", "D9", "D8", "D7", "E7",
"F7", "G7", "H7", "I7", "J7",
"K7", "K6", "L6", "L5", "L4",
"L3", "L2", "M2", "N2", "N3",
"N4", "N5", "N6", "N7", "N8",
"O8", "P8", "P7", "P6", "P5",
"P4", "P3", "P2", "P1", "Q1"};
int select;
disp_menu();
select = keyin.nextInt();
while(select != 4) {
switch(select) {
case 1:
disp_Stack();
break;
case 2:
for (int i=0; i<path.length; i++){
step = path[i];
if (push(step))
System.out.printf("%s ==> ", step);
else {
System.out.printf("目前路徑已滿請回頭!!\n");
break;
}
if ((i+1) %5 == 0)
System.out.printf("\n");
}
System.out.printf("總共走了 %d
路徑\n", Top+1);
break;
case 3:
int k = 0;
while (Top >= 0) {
step = pop();
System.out.printf("%s ==> ", step);
k = k + 1;
if(k%5 == 0)
System.out.printf("\n");
}
System.out.printf("回程路徑已結束\n");
break;
default:
System.out.printf("輸入錯誤 !!
請重新輸入\n");
}
disp_menu();
select = keyin.nextInt();
}
}
//
列印功能表
static void disp_menu() {
System.out.printf("==
歡迎光臨
走迷宮演練 ==\n");
System.out.printf("(1)
列印以走過的路線\n");
System.out.printf("(2)
迷宮去程開始\n");
System.out.printf("(3)
迷宮回程開始\n");
System.out.printf("(4)
離開系統\n");
System.out.printf("\t
請輸入工作選項 =>");
}
//
列印 Stack
內容
static void disp_Stack() {
System.out.printf("\n==
到目前經過 %d
個路徑 ==\n", Top+1);
for(int i=0; i<= Top; i++){
System.out.printf("(%d)%s ", i+1, Stack[i]);
if ((i+1) %5 == 0)
System.out.printf("\n");
}
}
//
加入 Push
元素
static boolean push(String step){
if (Top >= 50) {
return false;
}else {
Top = Top +1;
Stack[Top] = step;
return true;
}
}
static String pop(){
String step = Stack[Top];
Top = Top - 1;
return step;
}
} |
4-6-3 自我挑戰:迷宮闖關遊戲
(A) 程式功能:PM4_5.java
圖 4-22 是一張迷宮地圖,請編寫一只程式,使其能由 D9 進入後,由 Q3 出去,表示闖關成功,再顯示所有經過的路徑為何。
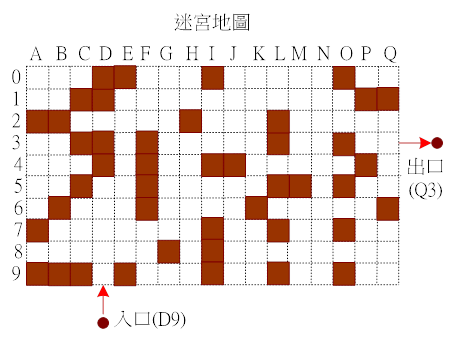
圖 4-23 迷宮地圖
(C) 系統分析
走迷宮最基本必須知道目前在哪一節點,可以往哪一個下一個節點走,以 G6 節點為例,下一個節點可以是 {G5, H6, G4, F6},亦是“(“G”± 1)(6 ± 1)。
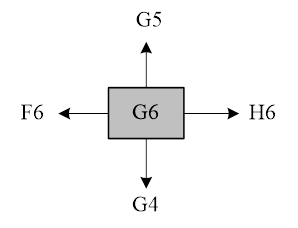
圖 4-23 節點的下一個節點
接著,我們必須知道哪些節點是可以通過的,我們用 path[] 來記錄可以經過的節點如下:(將迷宮地圖數位化)
Path[] = {A0, A1, A3, A4, A5, A6, A8, B0, B1, B3, B4, B5, B7, B8, C0,
C2, C4, C6, C7, C8, D2, D5, D6, D7, D8, D9, E1, E2, E3, E4,
E5, E6, E7, E8, F0, F1, F2, F7, F8, F9, G0, G1, G2, G3, G4,
G5, G6, G7, G9, H0, H1, H3, H4, H5, H6, H7, H8, H9, I1, I2,
I3, I5, I6, J0, J1, J2, J3, J5, J6, J7, J8, J9, K0, K1, K2, K3, K4,
K5, K7, K8, K9, L0, L1, L4, L6, L8, M0, M1, M2, M3, M4,
M6, M7, M8, M9, N0, N1, N2, N3, N4, N5, N6, N7, N8, N9
O1, O2, O4, O6, O8, P0, P2, P3, P5, P6, P7, P8, P9, Q0, Q2,
Q3, Q4, Q5, Q7, Q8, Q9}
當我到達某一節點後,計算出下一個路徑節點為何,再搜尋是否在 path[] 陣列內(扣除剛經過的節點),如果有則往下一個節點走,如果都沒有的話,則必須再退回上一個節點,再搜尋可以通過的節點。
僅提示到此,接著讓同學搜尋(Google 一下甚麼都有)其他方法實現它。
|

翻轉工作室:粘添壽
Java 程式設計(二) 含物件導向
翻轉電子書系列:
|
![]()